Intervalon 2D-Interval Explorer (musical instrument)

Intervalon is a quality musical instrument.

• a software that works on a Windows PC/tablet, a Win32 desktop application (freeware), with native Touch interface support.
• particularly good for (re)learning/researching most basic elements of music.

(very) unique features :

• Meantone tunings. (Enharmonics such as C#/Db, F#/Gb,.. are different things unlimitedly.)
• Harmonic-series tone note-keys
• Musical intervals have 2D-ness (two dimensional), as evident in meantone tunings.
  
  • They are notated by coordinates, using two intervals as the two basic elements.
    e.g. a second (1,0), third (2,0), minor third (0,1), fifth (2,1), octave (3,2);
    another way: a second (2,0), third (4,0), fifth (1,1), octave (0,2).
    
  • 2D Intervals and how they are tuned are naturally visualized by observing the linearities of both 2D Intervals and pitches.
    The board you see/play is nothing else. (C-D-E are straight only if tuned straight.)
    Harmonic-series tones are drawn by the same method, related with 2D Intervals.
• for Counterpoint practice: Self-, multi-voice, multi-take play.  (Don't try to play a full symphony with this.)
     simplest 2-voice sample:
     
• remarkable musical instrument engine (own): exact tunings, constant responses, customizability, very low resource usage, etc.

Before getting started, a minute about Meantone tunings :

• (basic ones)
  • 0 Meantone :  Pythagorean tuning (called 0 Meantone in this context), has pure fifth, harmonic-series #2-#3.
  • 1 Meantone :  has pure third, #8-#10.
• (how far/near from the above two)
  • 4/3 Meantone : has pure minor third, #10-#12, or pure sixth #3-#5, so basically important.
  • 2 Meantone : harmonic-series #9-#10 is its second. (2 is double far from 0 than 1.)
  • 7/6 Meantone : mean of 4/3 and 1 Meantones. 7/6 = (1+(4/3))/2
  • 7/12 Meantone : mean of 7/6 and 0 Meantones. fifth 698.81867 cents. 5th/3ths/6ths balancedly unpure.
  • and many intermediate ones.

Getting started :

• Download the zip file (Intervalon20210502.zip, 9.5MB) containing the latest Intervalon folder.
• (After security scan by your antivirus software, and checking with VirusTotal site for double sure,)
  unblock the zip file (right-click → Properties → Unblock),
  then unzip it (right-click → Open → drag the IntervalonYYYYMMDD folder to say, Desktop).
• The folder has in it
  • Intervalon.exe,
  • three DLL files (un4seen Bass Audio Library),
  • Intervalon.ini,
  • text files with additional info,
  • 'Soundfonts' folder,
  • 'Projects' folder (for self-,multi-voice,multi-take play)
  You can put the Intervalon folder (or later move it) anywhere you like.
• 'Soundfonts' folder initially contains a small soundfont of my compilation/modification, EditedforIntervalon.sf2.
  It has a little more than 20 instrument tones (presets). Acknowledgements is in More Info.txt file.
• You can use your favorite soundfonts (.sf2, .sfz).
  Make shortcut files of them and put the shortcuts in the 'Soundfonts' folder.
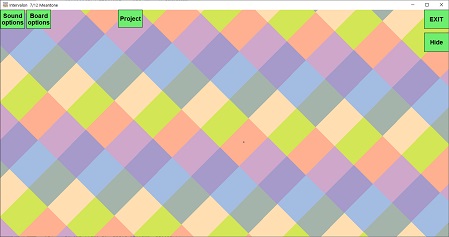
• Open (run) Intervalon.exe. Administrative privileges are not required. The board window appears.

  
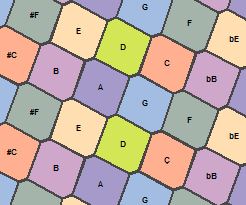
    The dotted button is middle C.
    In the initial setting, you play middle C-D-E mid-board.
    C,C#,C##...,Cb,Cbb,Cbbb.. share the same button color.

  Now you can play (just touch note-key buttons, or press PC keyboard keys), and change settings.
  Messages are displayed at the bottom of the window.
  For example, if you keep pressing two note-keys at the same time (cord), the interval and cents between them are displayed.


• First, resize the window.
• Then, press 'Board options' button at the top-left corner of the window.
  
  • (If the window is vertically not large enough to show all lines, you can kind of scroll by pressing the twin buttons at the right of 'Board options' button.)
  • (Buttons with paired arrows on them go forward/backward with larger steps.)
  • (Pressing 'Hide' button at the top-right corner of the window hides (or unhides) everything other than note-key buttons.)
  • Adjust scaling by the buttons on the 'Scaling' line, first 'overall', then 'note-keys'.
  • Scroll (change the note range covered) by the buttons on the 'scroll' line.
  • You can change the board layout.  A couple of prototype patterns (Layout profiles) are provided.
    Note that you can extend the note-key range to eg. six octaves, even with a small window, by changing x:y ratio.
  • Save the board settings into the ini file by pressing 'save options' button at the window top.
    This software does not save options automatically at program exit.

  
  (x:y ratio 275.  'Button looks' adjusted.)
  

• Press 'Sound options' button.
  
  • Select a tuning to be played in.
    
    • To select an irregular tuning such as Werckmeister, check 'uneven'.  (You can shift up/downs.)
  • Select an audio device, a soundfont, an instrument tone (a preset in the soundfont).
  • Alternately, you can use an external midi software/hardware multitimbral synthesizer. (Your electric piano might be one.)
    Check 'external synth' button, then select the synth (midi-out device).
  • Save the sound settings into the ini file by pressing 'save options' button.
    This software does not save options automatically at program exit.
  
  
• Play Harmonic-series tones :
  • 'Board options' → check 'Harmonic-series tones' button.
    Harmonic-series tone note-keys are drawn on the board based on their pitch heights and intervals given.
  • Specify the primary (first) tone by mounting a harmonic-series tone button on any board note-key button.
    'Board options' → check 'Drag' → drag → uncheck 'Drag'
  • Alternately 'HS Pad' can be used for easier playing.
  
  
• Adjust response times (latency) :
  • To go for very low latency levels, you can use Windows audio Exclusive-mode by simply checking 'exclusive' button.
    Event sub-mode is the default. If it does not work, switch to push-mode, by unchecking 'event mode'.
  • Response times are adjusted by two items in the sound profile, 'audio latency (minimum)' and 'delay note-off'.
    A sound profile has many items but there are on screen only two lines for them, so change items displayed as needed.
  
  
• Augment instrument tones :
  • 'Sound options' → check a button under 'Augment voice by supplimentary note-on's' → select an interval.
  • You can optionally use an auxiliary, second instrument tone;
    • Check 'Auxiliary Instrument', then after checking 'for Aux. instrumnet', select an instrument for the second tone.
  
  
• PC Keyboard playing :
  • A couple of key-mapping sets are provided.
  • First, select the keyboard physical layout nearest to yours. 'Board options' → 'PC keyboard key playing'.
  • Switch key mappings.
    • mapping type 'Next right always 2nd' :
      • If middle D is at the window center, Note-keys C-D-E-F are played by keyboard keys G-H-J-I  (K is F#).
      • If you scroll the board, note-keys played will change accordingly.
    • mapping type '2nd next right always Octave' :
      • If middle D is at the window center, C-D-E-F are played by keyboard keys 7-U-J-M.
      • If you scroll the board, note-keys played will change accordingly.
    • mapping type 'Harmonic-series tones' :
      • Harmonic-series tones #1,#2,....are played by keyboard keys Q,W,E,R,T,....
      • #8,9,10... are also played by A,S,D...
  • Mouse playing :
    • The primary interface is mousewheel → move (hover) → mousewheel.  See More Info.txt.
  
  
• Self-, multi-voice, multi-take play :
  • Press Project button, then select a project.
  • 'front' voice is the voice you are going to play.
  • You play front voice listening to your past plays in the voice (past takes) if any, and your past plays in other 'back' voices.
  • You can also make a wav file of your play.